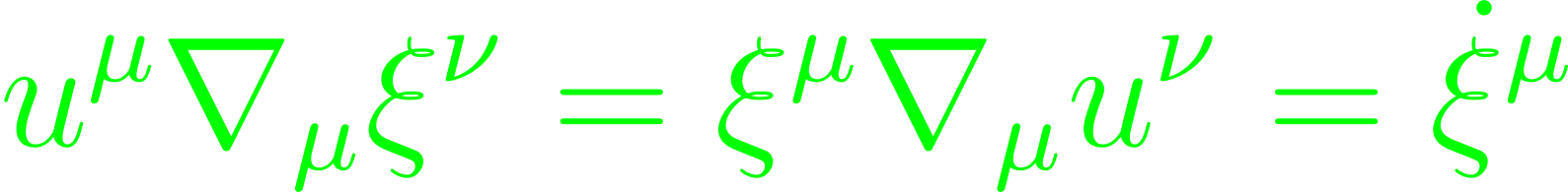Relativistic Hydrodynamics 2026, 06: Relativistic Perfect Fluids

In helping with describing the kinematics of a fluid, define the displacement vector as the 4-vector connecting two infinitesimally close fluid elements moving along wordlines. It has a rate of change defined through the fluid velocity, and from which emerges the convective derivative.

Those lines, along which the convective derivative is constant, are referred to as "fluidlines" of a fluid element, meaning the streamlines of an integral curve. The definition can be expanded using the projection tensor onto the hypersurface orthogonal to the velocity vector.

where ω is the kinematic vorticity tensor, σ the shear tensor and θ the expansion scalar, which define the volume transformations available to a fluid element (or any spatial element with a (unit) volume).

The simplest current is the rest-mass density current J, which is a 4-vector analogous to the energy-momentum tensor, and partially defined in its terms. The definition for the spatial stress tensor L follows from the projection tensor.

For perfect fluids,

A perfect fluid is isentropic when the derivative itself evaluates to 0. The four vector Q = T·ξ is a conserved quantity. At this point it becomes very convenient that I've read the aerodynamics book, because those classifications return at this point, along with some of the basic tools, which will be expanded into their relativistic counterparts.

In general, relativistic hydrodynamics can be approached from velocity-potentials which defines the integrals of motions as products of quantities with the velocity vectors, and a variational principle, which is strongly reminiscent of the principle of least action from classical mechanics.