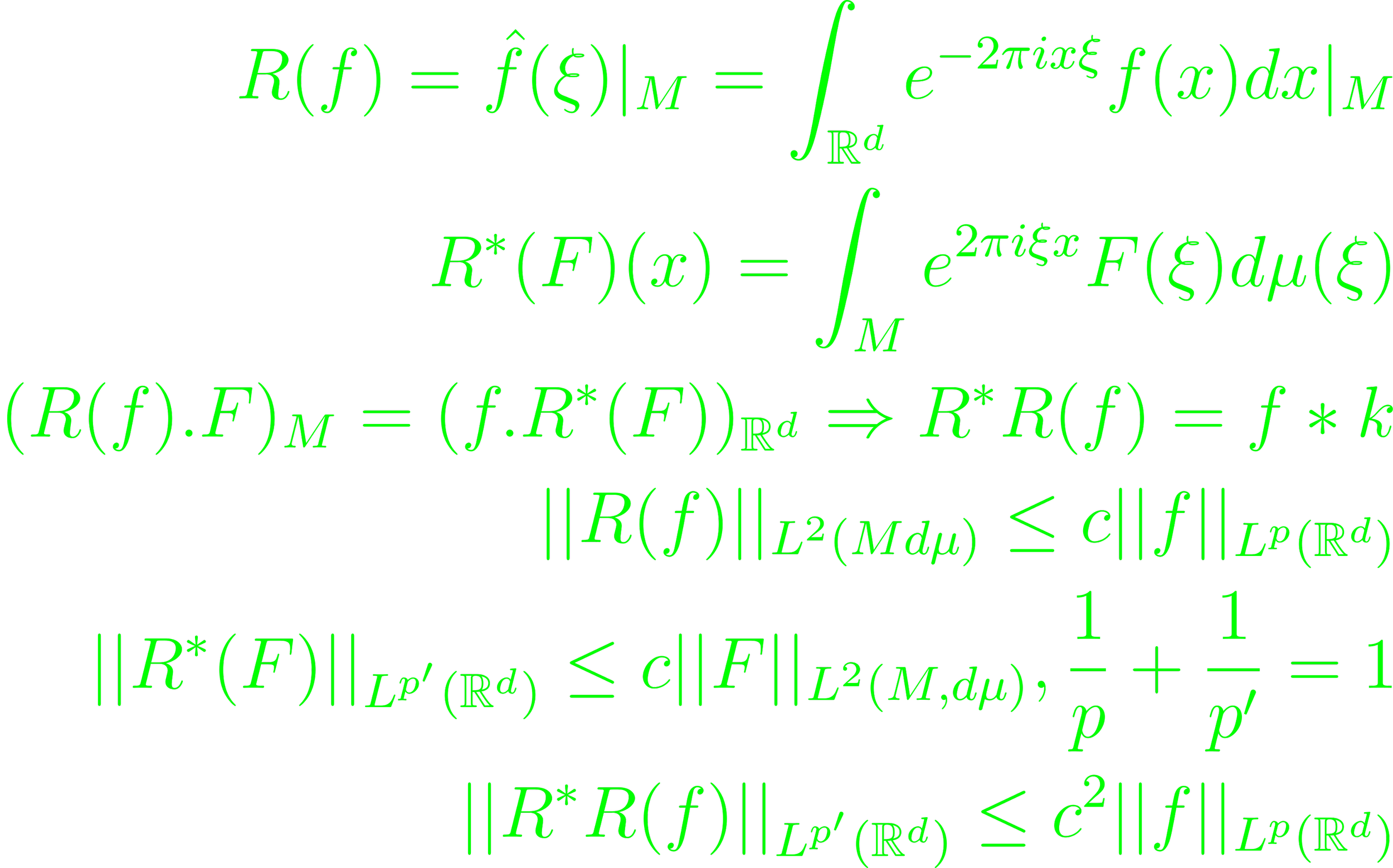Functional Analysis 2024, 25: Restriction Theorems

The Fourier transform of an L1-function f is continuous, and simultaneously, according to Hausdorff-Young, it belongs to Lq for f in Lp 1 ≤ p ≤ 2, 1/q + 1/p = 1. The Lq-functions are determined almost everywhere, so said Fourier transformation can't be meaningfully defined on an Lp-function. 1 < p ≤ 2. The Fourier-transformation are in this way not generally self-dual. If f is a radial function, the its Fourier-transform is continuous, if 1 ≤ p < 2d/(d+1). For non-radial f, this relation is not as straight-forward.

To inspect this problem, fix a local hypersurface M in ℝᵈ first, then phrase the restriction problem through a surface-carried measure dμ = φdσ. Assume 1 < p < 2, then there needs to be a q with

for an appropriately dense class of Lp-functions with an independent bound c. The condition is referred to as the (Lp, Lq)-restriction holding for M. If M has a non-zero Gauss curvature at each point of the support dμm then the below restriction inequality holds

The sequence p tends to 2. Given a p ≥ 1, define a norm R, with three equivalent norm statements

By this, the restriction property holds both for