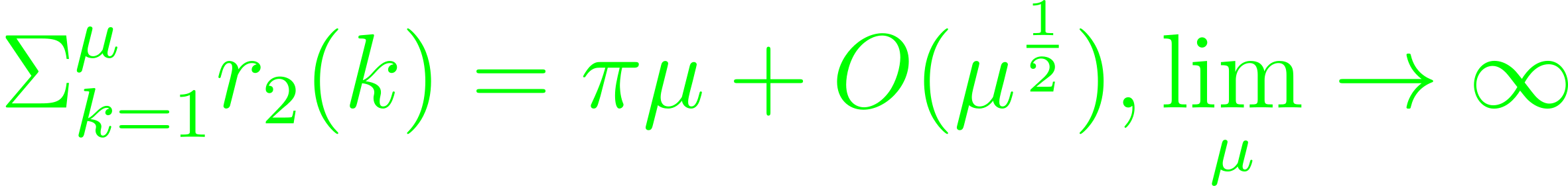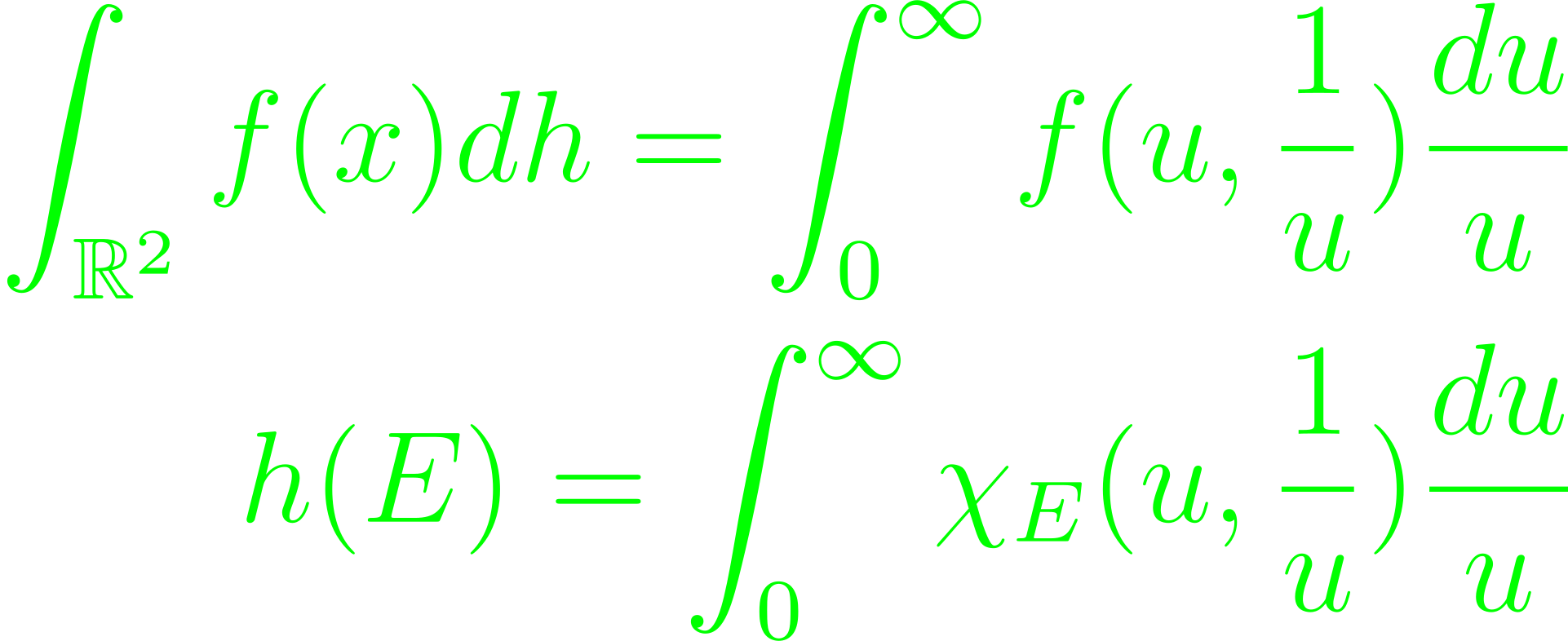Functional Analysis 2024, 27: Counting Lattice Points

Take first arithmetic functions r₂(k) that map a number k to sums of two squares, and d(k) ones that are divisors of k. These are highly irregular at first glance. By Gauss,

Also, for functions f from the Schwartz-space

with ℤᵈ the collection of lattice points, and the hat denoting the Fourier transform. If a set Ω is convex and bounded with the C² boundary, then defining functions ρ for Ω are second fundamental forms is positive semi-definite. This makes Ω "strongly convex", if the quadratic form is strictly positive definite at each point of the boundary of Ω. If it also has a sufficiently smooth boundary, and 0 is part of Ω, then the number of lattice point can be defined through

To prove the statement for the divisor function, one requires the hyperbolic measure dh on ℝ²

which can be used to decompose the problems into positive and negative oscillatory integrals J. Note the quadrants of the ℝ² plane with the letter Q, for the purposes of examining the Fourier transforms of J. With it, one can define a hyperbolic summation formula.