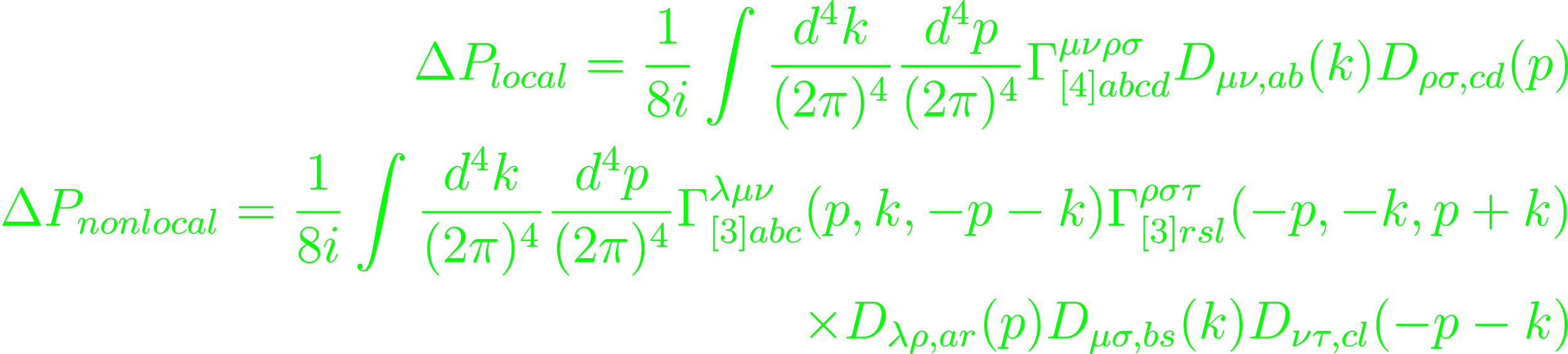YM-Thermodynamics 2024, 29: Effective Radiative Corrections
The Feynman rules in unitary-Coulomb gauge in SU(2) are derived by letting g approach e. The real-time formulation of finite-temperature field theory can thus separated thermal flux from the quantum fluctuations.
The delta functions of the same argument can be resummed after loop-expansion. The problem of pinch-singularities occurs in ring diagrams / daisy diagrams. Since no momentum transfer takes place in TLM propagators across the 4-verticies in a daisy diagram, the thermal component of the line is associated in a delta function of the same argument. Each such line adds a power in which the delta function occurs. The resummation is handled via the screening functions for TLM and TLH at tree-level
It follows that if an imaginary component exists, then the powers of the δ-functions with the same argument relax to powers of finite width peaks, which are mathematically well defined. The imaginary part arises in the screening functions for TLM, TLH modes at higher irreducible loop orders. This broadens the delta function and the emergence of the screening functions at 1-loop order slightly changes tree-level constraints at higher loop order.
The exact propagator fixes the exact dispersion law of each mode, but requires knowledge of all contributing diagrams to the mode's full propagator. In momentum space, connected bubble diagrams can be removed by cutting an internal line of momentum, which implies that the removed bubble's contribution is zero. Connected bubble diagrams that are nonvanishing thus are those, which have all 1PI contributions to the polarization tensors resummed. The number of independent loop momenta L, thee number of internal lines I, and the number of vertices for planar bubble diagrams V stand in following relation: L = I - V + 1.
The constraints levelled at these quantities are independent inequalities, so they don't directly identify independent hypersurfaces, rather, they "fatten" the hypersurfaces through the wiggle room introduced by the inequality.
The 2-loop correction follows in schema the one from QFT by separating the pressure into its nonlocal and local contribution.
Summing over Lie-algebra indices and contracting the Lorentz indices with the TLH propagators renders the integration over the zero components of the loop momenta trivial. 3-loop estimates are best achieved numerically.