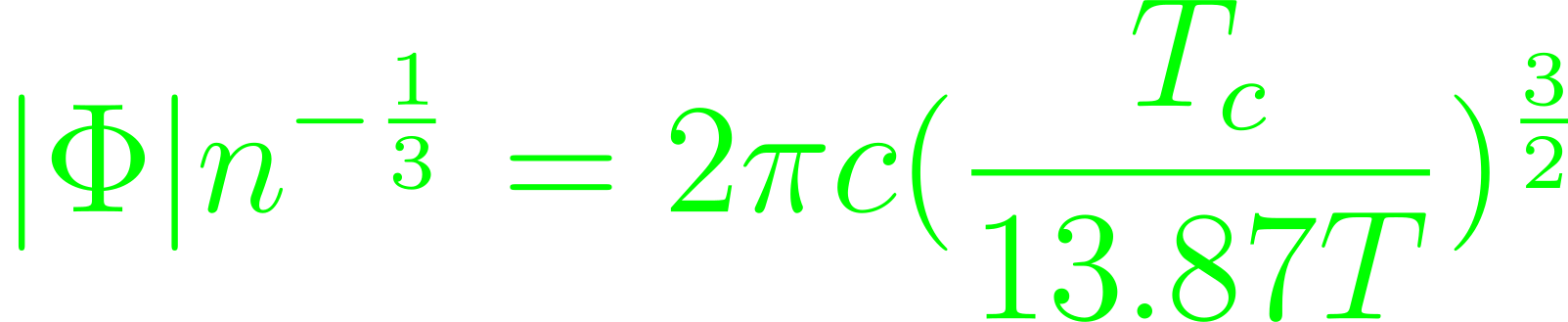YM-Thermodynamics 2024, 31: Stable, Screened Magnetic Monopoles
The magnetic (anti-)monopoles are liberated by the disscociation of (anti-)calorons via the radiation interaction, shifting the holonomy. At high temperatures a single 2-loop pressure-correction contains most of the information on the physics of stable monopoles created this way. Short-lived monopole-antimonopole pairs of small-holonomy calorons are described by pure-gauge configurations of the ground-state of the effective theory.
On distances larger than the minimal spatial length, without taking into account radiatively liberated stable and isolated monopole-antimonopole pairs, the depletion of a single magnetic test charge by instable magnetic monopole above critical temperature is described by the effective, electric coupling e = const, which in turn indicates that the modes are solely determined by topology and temperature. This may be conceived as a nonperturbative manifestation of asymptotic freedom. The constancy of e and the 2-loop correction to the pressure normed to non-dimensionality are approached in power-like speed of T. Asymptotic constancy of e is not the same as the behavior under fundamental gauge coupling. At high temperature, the holonomy-independent sum of the BPS mass are constituents of an (anti-)caloron of nontrivial holonomy.
This describes a pair of BPS-saturated (anti-)monopoles as test charges in a surrounding, where (anti-)calorons of small holonomy generate short-lived magnetic dipoles. This leads to a finite multiplicative charge renormalization for each of the particles. The underlying assumptions hold. A linear superposition of the U(1) monopole potentials then leads to a dipole form, decaying by 1/R³ over large distances R. In terms of the effective theory, this corresponds to the approximation of free and massless excitation and two massive free thermal quasiparticles plus the tree-level estimate of the thermal ground state. For the radiative corrections, screened & stable magnetic charges with some average distance is relevant. Define it as
which is less than unity for sufficiently high temperatures (resolution is estimated up to 1.91 times the critical temperature). In actuality, isolated and screened (anti-)monopoles are never fully resolved in the effective theory for the deconfining phase. The effect on the propagation of the tree-level massless gauge mode is sizable at temperatures multiple times the critical temperature. Screening produces a mass scale associated with an exponentially decaying U(1) potential. The collective long-distance effects are detectable, but never appear explicitly in the effective theory as a mathematical expression. For thermally fluctuating, free excitations as the asymptotic starting point, small interactions between the excitations as described by radiative corrections do not change the energy density of the effective, asymptotic 1-loop diagram. The radiative corrections to this 1-loop diagram must be canceled out by the effects generated by the unresolved thermodynamic degrees of freedom. (Anti-)Calorons dissociate upon strong quantum deformation into isolated magnetic monopole-antimonopole pairs, so these degrees of freedom are stable, screened magnetic (anti-)monopoles. The high-temperature 2-loop correction should be interpreted as the negative of a correction to the free quasiparticle pressure obtained by a thermal average over all domainized configurations of the field, and the result of the configuration is homogeneous in space. Due to the spatial coarse-graining, expect
so that the effect of all other screened, unresolved and stable (anti-)monopoles generated by the dissociation of (anti-)calorons of large holonomy is a lift of the mass by about 14% above the BPS bound. The hypothetical monopole density at high temperature